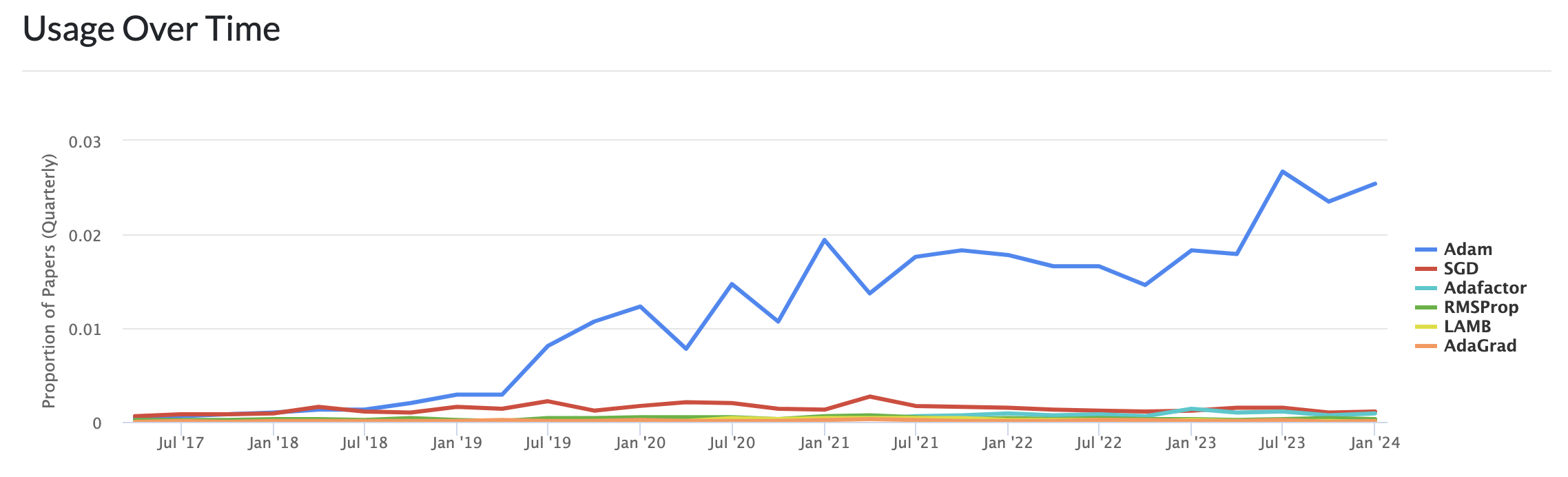
[Paper Exploration] Adam: A Method for Stochastic Optimization
Author: Diederik P. Kingma, Jimmy Ba
Published on 2014
Abstract
We introduce Adam, an algorithm for first-order gradient-based optimization of stochastic objective functions, based on adaptive estimates of lower-order moments. The method is straightforward to implement, is computationally efficient, has little memory requirements, is invariant to diagonal rescaling of the gradients, and is well suited for problems that are large in terms of data and/or parameters. The method is also appropriate for non-stationary objectives and problems with very noisy and/or sparse gradients. The hyper-parameters have intuitive interpretations and typically require little tuning. Some connections to related algorithms, on which Adam was inspired, are discussed. We also analyze the theoretical convergence properties of the algorithm and provide a regret bound on the convergence rate that is comparable to the best known results under the online convex optimization framework. Empirical results demonstrate that Adam works well in practice and compares favorably to other stochastic optimization methods. Finally, we discuss AdaMax, a variant of Adam based on the infinity norm.
Optimization
The goal of optimization is to minimize some function, given some constraints.
$min$ $f(x)$ $s.t.$ $x \in X $
- The vector $x = (x_1, . . . , x_n)$ is the optimization variable (or decision variable) of the problem
- The function $f$ is the objective function
- A vector $x$ is called optimal, of the problem, if it has the smallest objective value among all vectors that satisfy the constraints. Among all the feasible solutions (i.e., solutions that satisfy the constraints), an optimal solution is the one that achieves the best objective value (smallest for minimization problems, largest for maximization problems).
- $X$ is the set of inequality constraints
Mathematical ingredients:
- Encode decisions/actions as decision variables whose values we are seeking
- Identify the relevant problem data
- Express constraints on the values of the decision variables as mathematical relationships (inequalities) between the variables and problem data
- Express the objective function as a function of the decision variables and the problem data.
min or max f(x1, x2, .... , xn)
subject to gi(x1, x2, ...., ) <= bi i = 1,....,m
xj is continuous or discrete j = 1,....,n
The problem setting
- Finite number of decision variables
- A single objective function of decision variables and problem data
- Multiple objective functions are handled by either taking a weighted combination of them or by optimizing one of the objectives while ensuring the other objectives meet target requirements.
- The constraints are defined by a finite number of inequalities or equalities involving functions of the decision variables and problem data
- There may be domain restrictions (continuous or discrete) on some of the variables
- The functions defining the objective and constraints are algebraic (typically with rational coefficients)
Minimization vs Maximization
- Without the loss of generality, it is sufficient to consider a minimization objective since maximization of objective function is minimization of the negation of the objective function
Example: Designing a box:
Given a $1$ feet by $1$ feet piece of cardboard, cut out corners and fold to make a box of maximum volume:
Decision: $x$ = how much to cut from each of the corners?
Alternatives: $0<=x<=1/2$
Best: Maximize volume: $V(x) = x(1-2x)^2$ ($x$ is the height and $(1-2x)^2$ is the base, and their product is the volume)
Optimization formulation: $max$ $x(1-2x)^2$ subject to $0<=x<=1/2$ (which are the constraints in this case)
This is an unconstrained optimization problem since the constraint is a simple bound based.
Example: Data Fitting:
Given $N$ data points $(y_1, x_1)…(y_N, x_N)$ where $y_i$ belongs to $\mathbb{R}$ and $x_i$ belongs to $\mathbb{R}^n$, for all $i = 1..N$, find a line $y = a^Tx+b$ that best fits the data.
Decision: A vector $a$ that belongs to $\mathbb{R}^n$ and a scalar $b$ that belongs to $\mathbb{R}$
Alternatives: All $n$-dimensional vectors and scalars
Best: Minimize the sum of squared errors
Optimization formulation:
$\begin{array}{ll}\min & \sum_{i=1}^N\left(y_i-a^{\top} x_i-b\right)^2 \ \text { s.t. } & a \in \mathbb{R}^n, b \in \mathbb{R}\end{array}$
This is also an unconstrained optimization problem.
Example: Product Mix:
A firm make $n$ different products using $m$ types of resources. Each unit of product $i$ generates $p_i$ dollars of profit, and requires $r_{ij}$ units of resource $j$. The firm has $u_j$ units of resource $j$ available. How much of each product should the firm make to maximize profits?
Decision: how much of each product to make
Alternatives: defined by the resource limits
Best: Maximize profits
Optimization formulation:
Sum notation: $\begin{array}{lll}\max & \sum_{i=1}^n p_i x_i \ \text { s.t. } & \sum_{i=1}^n r_{i j} x_i \leq u_j & \forall j=1, \ldots, m \ & x_i \geq 0 & \forall i=1, \ldots, n\end{array}$
Matrix notation: $\begin{array}{cl}\max & p^{\top} x \ \text { s.t. } & R x \leq u \ & x \geq 0\end{array}$
Classification of optimization problems
- The tractability of a large scale optimization problem depends on the structure of the functions that make up the objective and constraints, and the domain restrictions on the variables.
| Optimization Problem | Description | Difficulty |
|---|---|---|
| Linear Programming | A linear programming problem involves maximizing or minimizing a linear objective function subject to a set of linear constraints | Easy to moderate |
| Nonlinear Programming | A nonlinear programming problem involves optimizing a function that is not linear, subject to a set of nonlinear constraints | Moderate to hard |
| Quadratic Programming | A quadratic programming problem involves optimizing a quadratic objective function subject to a set of linear constraints | Moderate |
| Convex Optimization | A convex optimization problem involves optimizing a convex function subject to a set of linear or convex constraints | Easy to moderate |
| Integer Programming | An integer programming problem involves optimizing a linear or nonlinear objective function subject to a set of linear or nonlinear constraints, where some or all of the variables are restricted to integer values | Hard |
| Mixed-integer Programming | A mixed-integer programming problem is a generalization of integer programming where some or all of the variables can be restricted to integer values or continuous values | Hard |
| Global Optimization | A global optimization problem involves finding the global optimum of a function subject to a set of constraints, which may be nonlinear or non-convex | Hard |
| Stochastic Optimization | A stochastic optimization problem involves optimizing an objective function that depends on random variables, subject to a set of constraints | Hard |
Convex Function (Why this matters?)

- “Function value at the average is less than the average of the function values”
- For a convex function the first order Taylor’s approximation is a global under estimator
-
A function $f: \mathbb{R}^n \rightarrow \mathbb{R}$ is convex if $$ f(\lambda \mathbf{x}+(1-\lambda) \mathbf{y}) \leq \lambda f(\mathbf{x})+(1-\lambda) f(\mathbf{y}) \quad \forall \mathbf{x}, \mathbf{y} \in \mathbb{R}^n \text { and } \lambda \in[0,1] $$
-
A convex optimization problem has a convex objective and convex set of solutions.
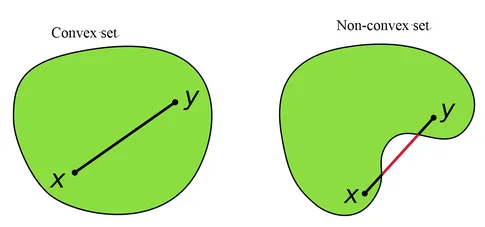
- Linear programs (LPs) can be seen as a special case of convex optimization problems. In an LP, the objective function and constraints are linear, which means that the feasible region defined by the constraints is a convex set. As a result, the optimal solution to an LP is guaranteed to be at a vertex (corner) of the feasible region, which makes it a convex optimization problem.
- A twice differentiable univariate function is convex if $f^{’’}(x)>=0$ for all $x \in R$
- To generalize, a twice differentiable function is convex if and only if the Hessian matrix is positive semi definite.
- The Hessian matrix of a function $f(x)$ with respect to the variables $x = (x_1, x_2, \ldots, x_n)$ is given by:

- A positive semi-definite (PSD) matrix is a matrix that is symmetric and has non-negative eigenvalues. In the context of a Hessian matrix, it represents the second-order partial derivatives of a multivariate function and reflects the curvature of the function. If the Hessian is PSD, it indicates that the function is locally convex, meaning that it has a minimum value in the vicinity of that point. On the other hand, if the Hessian is not PSD, the function may have a saddle point or be locally non-convex. The PSD property of a Hessian matrix is important in optimization, as it guarantees the existence of a minimum value for the function.
- $Hv=\lambda v$ (Remember this?)
Two steps of optimization
Most optimization algorithms have two main steps:
- Initialization: Create first solution to pick values for all of the variables (usually done randomly)
- Repeat a simple two-stage process:
- Starting with current solution, find a vector of relative changes to make to each variable. That is often called an improving direction.
- Make changes in that improving direction some amount, and that amount is called the step size.
- If the function is convex, it is guaranteed to find the minimal (since local is global)
Gradient Descent
- Iterative optimization algorithm used to find the minimum of a function, to update the parameters of a model during training.
- basic idea behind gradient descent is to adjust the parameters in the direction of steepest descent (negative gradient) to minimize a cost or loss function.
Objective Function : (also called a cost or loss function) that we want to minimize. Let’s denote the objective function as $J(θ)$, where $θ$ represents a vector of parameters that we want to optimize.
Initialization : Start by initializing the parameter vector θ with some arbitrary values (often with random values). This is the starting point of the optimization process.
Gradient Calculation : Calculate the gradient of the objective function with respect to the parameters. The gradient is a vector that points in the direction of the steepest increase in the function. Mathematically, the gradient is represented as:
$(\nabla J(\theta) = \left[\frac{\partial J(\theta)}{\partial \theta_1}, \frac{\partial J(\theta)}{\partial \theta_2}, \ldots, \frac{\partial J(\theta)}{\partial \theta_n}\right]) $
Here, $∂J(θ)/∂θ_i$ represents the partial derivative of $J(θ)$ with respect to the i-th parameter $θ_i$.
Update Parameters : Update the parameters θ using the gradient. The update rule is as follows:
$θ_{new} = θ_{old} - α * ∇J(θ_{old})$
Where:
- $θ_{new}$ is the updated parameter vector.
- $θ_{old}$ is the current parameter vector.
- $α$ (alpha) is the learning rate, a hyperparameter that controls the step size or how much to move in the direction of the gradient. It’s a small positive value typically chosen in advance.
This step is performed iteratively until a stopping criterion is met.
$\theta_{\text{ols}} = (X^T X)^{-1} X^T y$
import numpy as np
X = np.random.rand(100, 1)
y = 3 * X + 4
X_b = np.c_[np.ones((100, 1)), X]
theta_ols = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
intercept_ols = theta_ols[0][0]
slope_ols = theta_ols[1][0]
intercept_ols, slope_ols
>> (3.9999999999999987, 3.0000000000000004)
learning_rate = 0.01
n_iterations = 1000
theta_gd = np.random.randn(2, 1)
for iteration in range(n_iterations):
gradients = 2/100 * X_b.T.dot(X_b.dot(theta_gd) - y)
theta_gd = theta_gd - learning_rate * gradients
intercept_gd = theta_gd[0][0]
slope_gd = theta_gd[1][0]
intercept_gd, slope_gd
>> (4.102812626133385, 2.8119438961303405)
Accelerated Gradient Descent
- Add momentum to the mix
previous_gradient: holds the accumulated gradient from previous iterations. It is initialized as zeros or a vector of the same shape as the gradients.- keeping track of the sum of gradient
- Momentum might help escape local minima
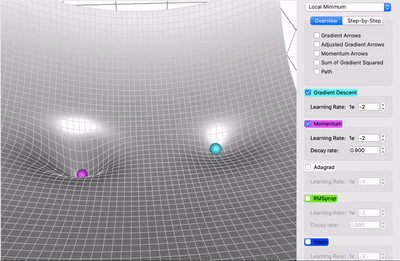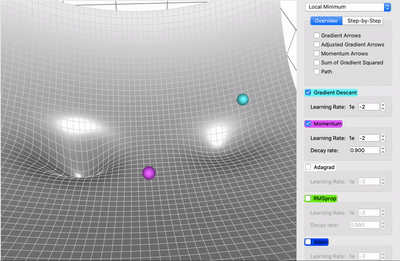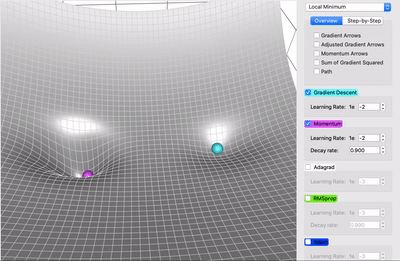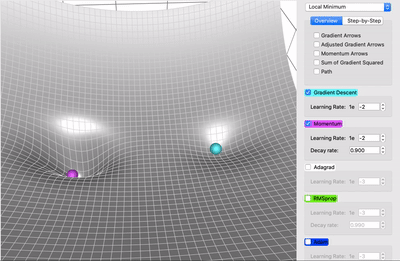
import numpy as np
X = np.random.rand(100, 1)
y = 3 * X + 4
X_b = np.c_[np.ones((100, 1)), X]
learning_rate = 0.01
n_iterations = 1000
momentum = 0.9
theta_gd = np.random.randn(2, 1)
previous_gradient = np.zeros_like(theta_gd)
for iteration in range(n_iterations):
gradients = 2/100 * X_b.T.dot(X_b.dot(theta_gd) - y)
previous_gradient = momentum * previous_gradient + (1 - momentum) * gradients
theta_gd = theta_gd - learning_rate * previous_gradient
intercept_gd = theta_gd[0][0]
slope_gd = theta_gd[1][0]
intercept_gd, slope_gd
>> (4.209787975619119, 2.619482953146455)
AdaGrad
- Adaptive Gradient algorithm
- Adagrad adapts the learning rate of each parameter based on the historical squared gradients. It scales the learning rate inversely proportional to the square root of the sum of squared gradients accumulated over time for each parameter.
- Adaptive learning rate for each parameter, allowing for larger updates for infrequent parameters and smaller updates for frequent parameters.
- Keep track of the sum of gradient squared and uses that to adapt the gradient in different directions
- The more you have updated a feature already, the less you will update it in the future, thus giving a chance for the others features (for example, the sparse features) to catch up.
- This property allows AdaGrad to escape a saddle point much better. AdaGrad will take a straight path, whereas gradient descent (or relatedly, Momentum) takes the approach of “let me slide down the steep slope first and maybe worry about the slower direction later”. Sometimes, vanilla gradient descent might just stop at the saddle point where gradients in both directions are 0 and be perfectly content there.
- Can become too aggressive in reducing the learning rate, causing premature convergence.
import numpy as np
X = np.random.rand(100, 1)
y = 3 * X + 4
X_b = np.c_[np.ones((100, 1)), X]
n_iterations = 1000
theta_adagrad = np.random.randn(2, 1)
G = np.zeros_like(theta_adagrad)
for iteration in range(n_iterations):
gradients = 2/100 * X_b.T.dot(X_b.dot(theta_adagrad) - y)
G += gradients ** 2
adjusted_gradients = gradients / np.sqrt(G)
theta_adagrad = theta_adagrad - adjusted_gradients
intercept_adagrad = theta_adagrad[0][0]
slope_adagrad = theta_adagrad[1][0]
intercept_adagrad, slope_adagrad
>> (3.9999984750713753, 3.0000027084018033)
RMSProp
- It uses a moving average of squared gradients to normalize the learning rate for each parameter.
- Instead of accumulating all past squared gradients, it uses an exponentially decaying average of past squared gradients.
- Mitigates the overly aggressive learning rate decay problem of Adagrad by using a decaying average of past squared gradients.
- Adagrad accumulates all past squared gradients, which can require more memory compared to RMSProp, which uses a decaying average.
- RMSProp is often preferred over Adagrad due to its better stability and performance
import numpy as np
X = np.random.rand(100, 1)
y = 3 * X + 4
X_b = np.c_[np.ones((100, 1)), X]
n_iterations = 1000
decay_rate = 0.8
theta_rmsprop = np.random.randn(2, 1)
G = np.zeros_like(theta_rmsprop)
for iteration in range(n_iterations):
gradients = 2/100 * X_b.T.dot(X_b.dot(theta_rmsprop) - y)
G = decay_rate * G + (1 - decay_rate) * gradients ** 2
adjusted_gradients = gradients / np.sqrt(G)
theta_rmsprop = theta_rmsprop - adjusted_gradients
intercept_rmsprop = theta_rmsprop[0][0]
slope_rmsprop = theta_rmsprop[1][0]
intercept_rmsprop, slope_rmsprop
ADAM
- Adaptive Moment Estimation
- Takes the best of both worlds of Momentum and RMSProp
- Adam gets the speed from momentum and the ability to adapt gradients in different directions from RMSProp
import numpy as np
X = np.random.rand(100, 1)
y = 3 * X + 4
X_b = np.c_[np.ones((100, 1)), X]
n_iterations = 1000
beta1 = 0.9
beta2 = 0.999
learning_rate = 0.01
theta_adam = np.random.randn(2, 1)
m = np.zeros_like(theta_adam)
v = np.zeros_like(theta_adam)
t = 0
for iteration in range(n_iterations):
t += 1
gradients = 2/100 * X_b.T.dot(X_b.dot(theta_adam) - y)
m = beta1 * m + (1 - beta1) * gradients
v = beta2 * v + (1 - beta2) * (gradients ** 2)
m_hat = m / (1 - beta1 ** t)
v_hat = v / (1 - beta2 ** t)
theta_adam = theta_adam - learning_rate * m_hat / np.sqrt(v_hat)
intercept_adam = theta_adam[0][0]
slope_adam = theta_adam[1][0]
intercept_adam, slope_adam
>> (3.4382879476383574, 4.0255351076360855)