The Beginner’s Trap
The stages in the analytics process is filled with moments of success and failures. There are some instant gratifications during the process, where a begginer like myself might construe a non success as success, due to some kind of judgement error.
This project will go through one of those instances and discuss some of the things I need to keep in mind so that I (and people new to analytics) do not make these mistakes.
The dataset is from https://www.kaggle.com/sanjeetsinghnaik/most-expensive-footballers-2021
Since learning is a never ending process, I will be updating the notebook (or creating a variation of it) as I discover more best practices. So, consider this to be an excerise on SOTA (State of the art) POC (proof of concept).
Steps involved:
- Introduction
- Exploratory Data Analysis
- Feature Engineering
- Linear Regression
- Decision Tree Regression
- Validation
- Conclusion
1. Introduction
The description of the dataset from Kaggle:
This file consists of data of Top 500 Most Expensive Footballer In 2021. The data is according to the prices listed in transfer market along with data like goals, assists, matches, age, etc.
The question we are trying to answer is:
** Based on different predictors (goals, assists, matches, age etc.) is it possible to predict the market value of footballers? **

The source of the image above is the Kaggle repository hosting the dataset.
Imports
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(rc={'figure.figsize':(12, 6)})
from matplotlib.ticker import MaxNLocator
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import cross_val_score
The dataset is in the file players_data.csv
df = pd.read_csv('players_data.csv')
Let us take a look at the columns. We have a few ways of doing this but I always found using list easy.
list(df)
['Name',
'Position',
'Age',
'Markey Value In Millions(£)',
'Country',
'Club',
'Matches',
'Goals',
'Own Goals',
'Assists',
'Yellow Cards',
'Second Yellow Cards',
'Red Cards',
'Number Of Substitute In',
'Number Of Substitute Out']
Since we know the dataset is a ranking of 500 highest paid footballers, the expected rows should be 500. And the number of columns is 15
df.shape
(500, 15)
Let’s look at the first few rows.
df.head()
| Name | Position | Age | Markey Value In Millions(£) | Country | Club | Matches | Goals | Own Goals | Assists | Yellow Cards | Second Yellow Cards | Red Cards | Number Of Substitute In | Number Of Substitute Out | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Kylian Mbappé | Centre-Forward | 22 | 144.0 | France | Paris Saint-Germain | 16 | 7 | 0 | 11 | 3 | 0 | 0 | 0 | 8 |
| 1 | Erling Haaland | Centre-Forward | 21 | 135.0 | Norway | Borussia Dortmund | 10 | 13 | 0 | 4 | 1 | 0 | 0 | 0 | 1 |
| 2 | Harry Kane | Centre-Forward | 28 | 108.0 | England | Tottenham Hotspur | 16 | 7 | 0 | 2 | 2 | 0 | 0 | 2 | 2 |
| 3 | Jack Grealish | Left Winger | 26 | 90.0 | England | Manchester City | 15 | 2 | 0 | 3 | 1 | 0 | 0 | 2 | 8 |
| 4 | Mohamed Salah | Right Winger | 29 | 90.0 | Egypt | Liverpool FC | 15 | 15 | 0 | 6 | 1 | 0 | 0 | 0 | 3 |
Let’s look at the last few rows.
df.tail()
| Name | Position | Age | Markey Value In Millions(£) | Country | Club | Matches | Goals | Own Goals | Assists | Yellow Cards | Second Yellow Cards | Red Cards | Number Of Substitute In | Number Of Substitute Out | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 495 | Giorgian de Arrascaeta | Attacking Midfield | 27 | 16.2 | Uruguay | Clube de Regatas do Flamengo | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 496 | Ayoze Pérez | Second Striker | 28 | 16.2 | Spain | Leicester City | 8 | 1 | 0 | 3 | 0 | 0 | 1 | 2 | 5 |
| 497 | Alex Meret | Goalkeeper | 24 | 16.2 | Italy | SSC Napoli | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 498 | Duje Caleta-Car | Centre-Back | 25 | 16.2 | Croatia | Olympique Marseille | 8 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 |
| 499 | Aritz Elustondo | Centre-Back | 27 | 16.2 | Spain | Real Sociedad | 15 | 3 | 0 | 1 | 4 | 0 | 0 | 1 | 1 |
2. Exploratory Data Analysis
Let’s use Pandas built in function to generate descriptive statistics
df.describe()
| Age | Markey Value In Millions(£) | Matches | Goals | Own Goals | Assists | Yellow Cards | Second Yellow Cards | Red Cards | Number Of Substitute In | Number Of Substitute Out | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 500.000000 | 500.000000 | 500.000000 | 500.000000 | 500.000000 | 500.00000 | 500.000000 | 500.000000 | 500.000000 | 500.000000 | 500.000000 |
| mean | 24.968000 | 31.537800 | 12.396000 | 2.160000 | 0.030000 | 1.51200 | 1.592000 | 0.036000 | 0.046000 | 2.394000 | 3.744000 |
| std | 3.165916 | 17.577697 | 4.342453 | 2.880102 | 0.170758 | 1.85276 | 1.445585 | 0.186477 | 0.209695 | 2.517825 | 3.293046 |
| min | 16.000000 | 16.200000 | 0.000000 | 0.000000 | 0.000000 | 0.00000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 23.000000 | 19.800000 | 10.000000 | 0.000000 | 0.000000 | 0.00000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 50% | 25.000000 | 25.200000 | 13.000000 | 1.000000 | 0.000000 | 1.00000 | 1.000000 | 0.000000 | 0.000000 | 2.000000 | 3.000000 |
| 75% | 27.000000 | 36.000000 | 16.000000 | 3.000000 | 0.000000 | 2.00000 | 2.000000 | 0.000000 | 0.000000 | 3.250000 | 6.000000 |
| max | 36.000000 | 144.000000 | 24.000000 | 23.000000 | 1.000000 | 12.00000 | 7.000000 | 1.000000 | 1.000000 | 13.000000 | 20.000000 |
Let us look into the data types for each of the columns
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 500 entries, 0 to 499
Data columns (total 15 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Name 500 non-null object
1 Position 500 non-null object
2 Age 500 non-null int64
3 Markey Value In Millions(£) 500 non-null float64
4 Country 500 non-null object
5 Club 500 non-null object
6 Matches 500 non-null int64
7 Goals 500 non-null int64
8 Own Goals 500 non-null int64
9 Assists 500 non-null int64
10 Yellow Cards 500 non-null int64
11 Second Yellow Cards 500 non-null int64
12 Red Cards 500 non-null int64
13 Number Of Substitute In 500 non-null int64
14 Number Of Substitute Out 500 non-null int64
dtypes: float64(1), int64(10), object(4)
memory usage: 58.7+ KB
Count of missing values
df.isna().sum()
Name 0
Position 0
Age 0
Markey Value In Millions(£) 0
Country 0
Club 0
Matches 0
Goals 0
Own Goals 0
Assists 0
Yellow Cards 0
Second Yellow Cards 0
Red Cards 0
Number Of Substitute In 0
Number Of Substitute Out 0
dtype: int64
df.isna().sum().sum()
0
We do not have any values missing from the dataset.
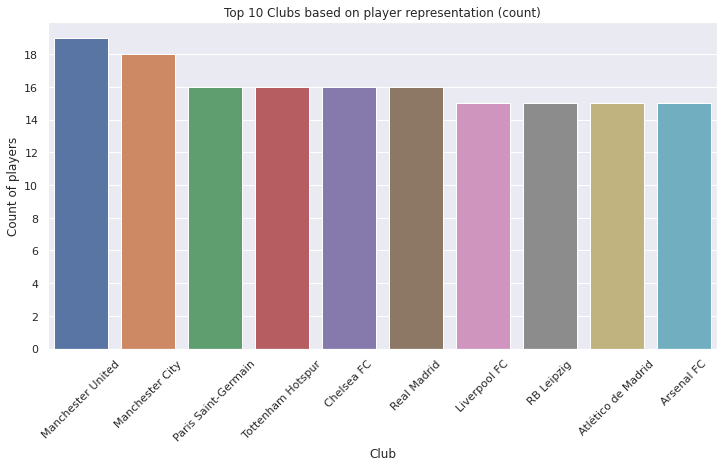
df.groupby('Club').size().sort_values(ascending=False).head(10)
Club
Manchester United 19
Manchester City 18
Chelsea FC 16
Tottenham Hotspur 16
Real Madrid 16
Paris Saint-Germain 16
RB Leipzig 15
Arsenal FC 15
Liverpool FC 15
Atlético de Madrid 15
dtype: int64
ax = sns.countplot(x='Club', data=df, order=df.Club.value_counts().iloc[:10].index)
ax.tick_params(axis='x', rotation=45)
ax.yaxis.set_major_locator(MaxNLocator(integer=True))
ax.set(xlabel='Club', ylabel='Count of players')
plt.title("Top 10 Clubs based on player representation (count)")
plt.show()
club_grouped = df.groupby(['Club'])[['Markey Value In Millions(£)']].sum().sort_values(by='Markey Value In Millions(£)', ascending=False).head(10)
club_grouped
| Markey Value In Millions(£) | |
|---|---|
| Club | |
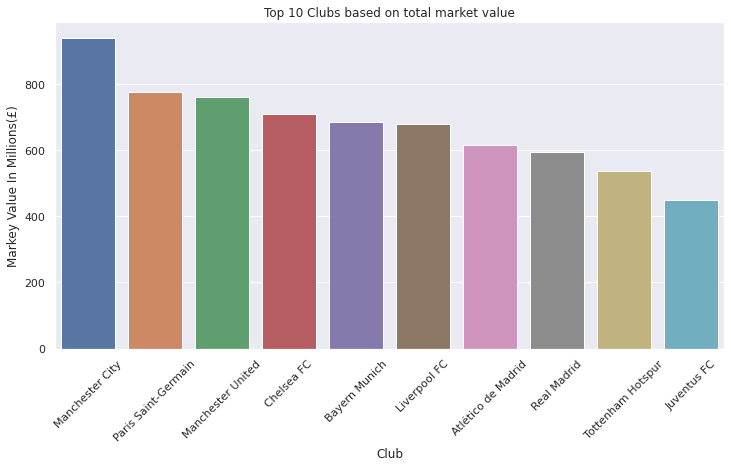
| Manchester City | 940.5 |
| Paris Saint-Germain | 775.8 |
| Manchester United | 760.5 |
| Chelsea FC | 709.2 |
| Bayern Munich | 685.8 |
| Liverpool FC | 681.3 |
| Atlético de Madrid | 616.5 |
| Real Madrid | 594.0 |
| Tottenham Hotspur | 536.4 |
| Juventus FC | 450.0 |
ax = sns.barplot(x=club_grouped.index, y=club_grouped['Markey Value In Millions(£)'])
ax.tick_params(axis='x', rotation=45)
ax.set(xlabel='Club', ylabel='Markey Value In Millions(£)')
plt.title("Top 10 Clubs based on total market value")
plt.show()
df.groupby('Country').size().sort_values(ascending=False).head(10)
Country
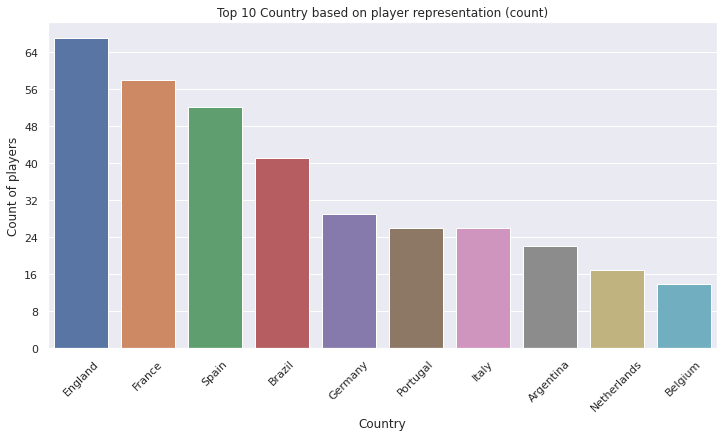
England 67
France 58
Spain 52
Brazil 41
Germany 29
Portugal 26
Italy 26
Argentina 22
Netherlands 17
Belgium 14
dtype: int64
ax = sns.countplot(x='Country', data=df, order=df.Country.value_counts().iloc[:10].index)
ax.tick_params(axis='x', rotation=45)
ax.yaxis.set_major_locator(MaxNLocator(integer=True))
ax.set(xlabel='Country', ylabel='Count of players')
plt.title("Top 10 Country based on player representation (count)")
plt.show()
country_grouped = df.groupby(['Country'])[['Markey Value In Millions(£)']].sum().sort_values(by='Markey Value In Millions(£)', ascending=False).head(10)
country_grouped
| Markey Value In Millions(£) | |
|---|---|
| Country | |
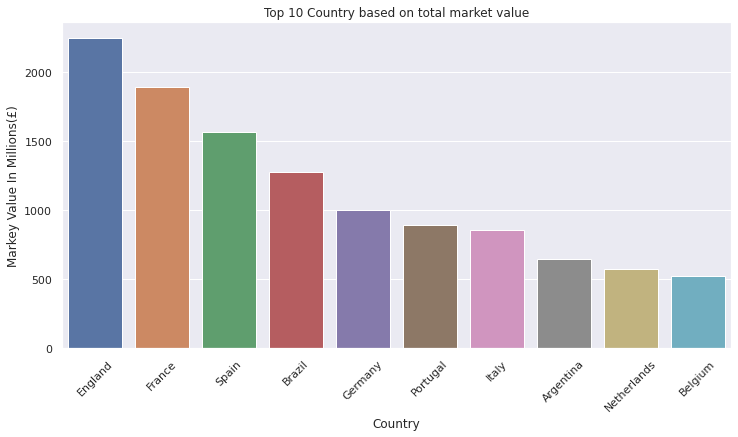
| England | 2248.2 |
| France | 1895.4 |
| Spain | 1565.1 |
| Brazil | 1275.3 |
| Germany | 1005.3 |
| Portugal | 890.1 |
| Italy | 854.1 |
| Argentina | 650.7 |
| Netherlands | 571.5 |
| Belgium | 522.9 |
ax = sns.barplot(x=country_grouped.index, y=country_grouped['Markey Value In Millions(£)'])
ax.tick_params(axis='x', rotation=45)
ax.set(xlabel='Country', ylabel='Markey Value In Millions(£)')
plt.title("Top 10 Country based on total market value")
plt.show()
df.groupby('Position').size().sort_values(ascending=False)
Position
Centre-Back 87
Central Midfield 74
Centre-Forward 70
Right Winger 48
Left Winger 46
Attacking Midfield 41
Defensive Midfield 41
Right-Back 30
Left-Back 23
Goalkeeper 19
Left Midfield 8
Second Striker 8
Right Midfield 5
dtype: int64
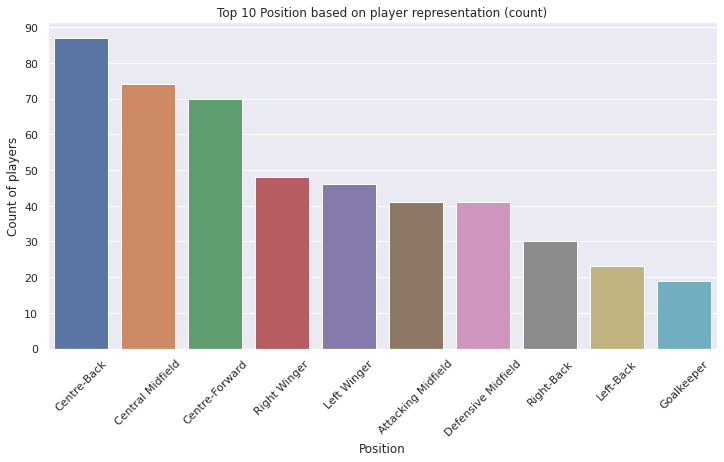
ax = sns.countplot(x='Position', data=df, order=df.Position.value_counts().iloc[:10].index)
ax.tick_params(axis='x', rotation=45)
ax.yaxis.set_major_locator(MaxNLocator(integer=True))
ax.set(xlabel='Position', ylabel='Count of players')
plt.title("Top 10 Position based on player representation (count)")
plt.show()
position_grouped = df.groupby(['Position'])[['Markey Value In Millions(£)']].sum().sort_values(by='Markey Value In Millions(£)', ascending=False).head(10)
position_grouped
| Markey Value In Millions(£) | |
|---|---|
| Position | |
| Centre-Back | 2583.9 |
| Central Midfield | 2421.9 |
| Centre-Forward | 2369.7 |
| Left Winger | 1647.0 |
| Right Winger | 1461.6 |
| Attacking Midfield | 1332.0 |
| Defensive Midfield | 1275.3 |
| Right-Back | 784.8 |
| Left-Back | 704.7 |
| Goalkeeper | 585.9 |
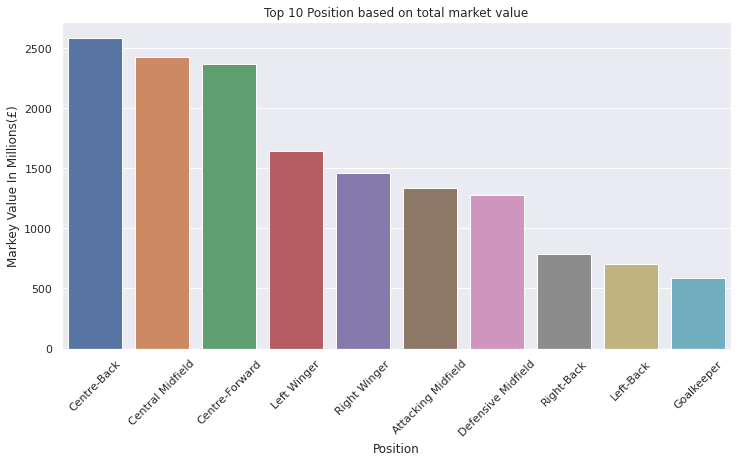
ax = sns.barplot(x=position_grouped.index, y=position_grouped['Markey Value In Millions(£)'])
ax.tick_params(axis='x', rotation=45)
ax.set(xlabel='Position', ylabel='Markey Value In Millions(£)')
plt.title("Top 10 Position based on total market value")
plt.show()
3. Feature Engineering
Since we only have 500 rows of data, 10 different positions, let us aggregate some of these positions together.
I created a simple position mapping and transformed it so that it was possible to use map
position_mapping = {
"forward" : ['Centre-Forward', 'Second Striker'],
"midfield" : ['Central Midfield', 'Attacking Midfield', 'Defensive Midfield', 'Left Midfield', 'Right Midfield', 'Right Winger', 'Left Winger'],
"back" : ['Centre-Back', 'Right-Back', 'Left-Back']
}
The only position we have not mapped here is Goalkeeper, which we will remove later on.
mapping_dict = {}
for key in position_mapping:
for item in position_mapping[key]:
mapping_dict[item] = key
mapping_dict
{'Centre-Forward': 'forward',
'Second Striker': 'forward',
'Central Midfield': 'midfield',
'Attacking Midfield': 'midfield',
'Defensive Midfield': 'midfield',
'Left Midfield': 'midfield',
'Right Midfield': 'midfield',
'Right Winger': 'midfield',
'Left Winger': 'midfield',
'Centre-Back': 'back',
'Right-Back': 'back',
'Left-Back': 'back'}
I could have just typed in the mapping_dict directly but this felt more natural.
df['Position_Agg'] = df.Position.map(mapping_dict)
df
| Name | Position | Age | Markey Value In Millions(£) | Country | Club | Matches | Goals | Own Goals | Assists | Yellow Cards | Second Yellow Cards | Red Cards | Number Of Substitute In | Number Of Substitute Out | Position_Agg | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Kylian Mbappé | Centre-Forward | 22 | 144.0 | France | Paris Saint-Germain | 16 | 7 | 0 | 11 | 3 | 0 | 0 | 0 | 8 | forward |
| 1 | Erling Haaland | Centre-Forward | 21 | 135.0 | Norway | Borussia Dortmund | 10 | 13 | 0 | 4 | 1 | 0 | 0 | 0 | 1 | forward |
| 2 | Harry Kane | Centre-Forward | 28 | 108.0 | England | Tottenham Hotspur | 16 | 7 | 0 | 2 | 2 | 0 | 0 | 2 | 2 | forward |
| 3 | Jack Grealish | Left Winger | 26 | 90.0 | England | Manchester City | 15 | 2 | 0 | 3 | 1 | 0 | 0 | 2 | 8 | midfield |
| 4 | Mohamed Salah | Right Winger | 29 | 90.0 | Egypt | Liverpool FC | 15 | 15 | 0 | 6 | 1 | 0 | 0 | 0 | 3 | midfield |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 495 | Giorgian de Arrascaeta | Attacking Midfield | 27 | 16.2 | Uruguay | Clube de Regatas do Flamengo | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | midfield |
| 496 | Ayoze Pérez | Second Striker | 28 | 16.2 | Spain | Leicester City | 8 | 1 | 0 | 3 | 0 | 0 | 1 | 2 | 5 | forward |
| 497 | Alex Meret | Goalkeeper | 24 | 16.2 | Italy | SSC Napoli | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | NaN |
| 498 | Duje Caleta-Car | Centre-Back | 25 | 16.2 | Croatia | Olympique Marseille | 8 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | back |
| 499 | Aritz Elustondo | Centre-Back | 27 | 16.2 | Spain | Real Sociedad | 15 | 3 | 0 | 1 | 4 | 0 | 0 | 1 | 1 | back |
500 rows × 16 columns
Now we can remove goalkeepers (which are NaNs because of missing mapping)
df.dropna(inplace=True)
Let’s create similar charts for the new column as well
df.groupby('Position_Agg').size().sort_values(ascending=False)
Position_Agg
midfield 263
back 140
forward 78
dtype: int64
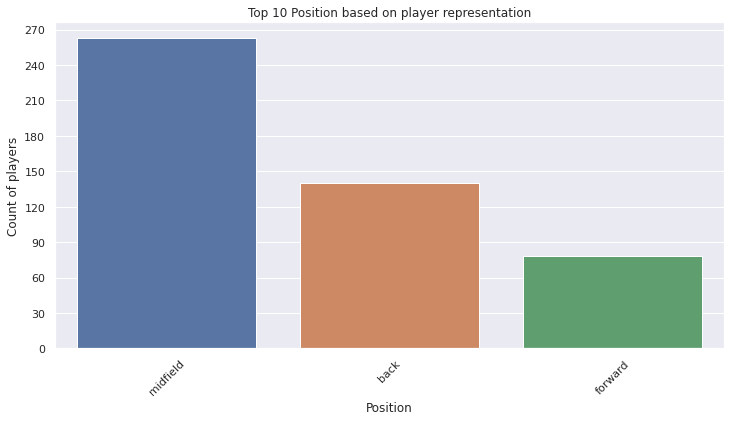
ax = sns.countplot(x='Position_Agg', data=df, order=df.Position_Agg.value_counts().iloc[:10].index)
ax.tick_params(axis='x', rotation=45)
ax.yaxis.set_major_locator(MaxNLocator(integer=True))
ax.set(xlabel='Position', ylabel='Count of players')
plt.title("Top 10 Position based on player representation")
plt.show()
position_agg_grouped = df.groupby(['Position_Agg'])[['Markey Value In Millions(£)']].sum().sort_values(by='Markey Value In Millions(£)', ascending=False).head(10)
position_agg_grouped
| Markey Value In Millions(£) | |
|---|---|
| Position_Agg | |
| midfield | 8460.0 |
| back | 4073.4 |
| forward | 2649.6 |
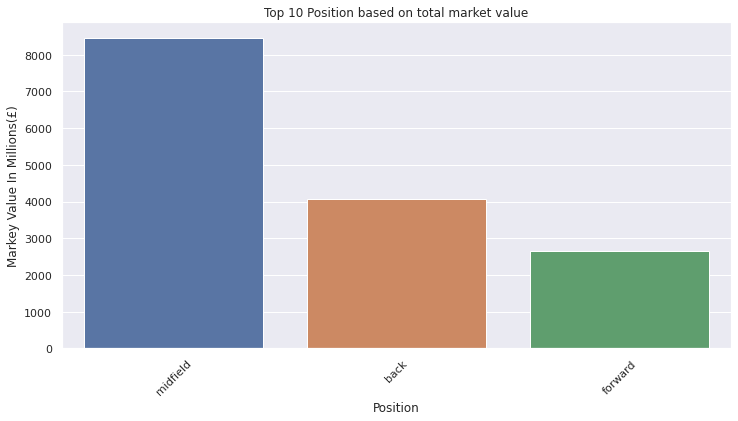
ax = sns.barplot(x=position_agg_grouped.index, y=position_agg_grouped['Markey Value In Millions(£)'])
ax.tick_params(axis='x', rotation=45)
ax.set(xlabel='Position', ylabel='Markey Value In Millions(£)')
plt.title("Top 10 Position based on total market value")
plt.show()
4. Linear Regression
First of all, let us only focus on the midfield players. Midfield is the largest group of players we have, and it might make more sense to use regression the same group of players.
df_mid = df[df.Position_Agg=='midfield']
df_mid.reset_index(drop=True, inplace=True)
list(df_mid)
['Name',
'Position',
'Age',
'Markey Value In Millions(£)',
'Country',
'Club',
'Matches',
'Goals',
'Own Goals',
'Assists',
'Yellow Cards',
'Second Yellow Cards',
'Red Cards',
'Number Of Substitute In',
'Number Of Substitute Out',
'Position_Agg']
df_mid = df_mid[['Age', 'Goals', 'Assists', 'Markey Value In Millions(£)']]
df_mid = df_mid.apply(lambda x: x/x.max(), axis=0)
df_mid
| Age | Goals | Assists | Markey Value In Millions(£) | |
|---|---|---|---|---|
| 0 | 0.764706 | 0.133333 | 0.3 | 1.00 |
| 1 | 0.852941 | 1.000000 | 0.6 | 1.00 |
| 2 | 0.882353 | 0.200000 | 0.1 | 1.00 |
| 3 | 0.852941 | 0.200000 | 0.3 | 1.00 |
| 4 | 0.617647 | 0.000000 | 0.0 | 0.90 |
| ... | ... | ... | ... | ... |
| 258 | 0.676471 | 0.066667 | 0.1 | 0.18 |
| 259 | 0.764706 | 0.000000 | 0.0 | 0.18 |
| 260 | 0.823529 | 0.000000 | 0.1 | 0.18 |
| 261 | 0.764706 | 0.200000 | 0.1 | 0.18 |
| 262 | 0.794118 | 0.000000 | 0.0 | 0.18 |
263 rows × 4 columns
X = df_mid.iloc[:, :-1]
y = df_mid.iloc[:, -1]
linear_regressor = LinearRegression().fit(X, y)
linear_regressor.score(X, y)
0.06775382996413992
linear_regressor.predict(X)
array([0.37728587, 0.61138884, 0.3870485 , 0.40721923, 0.28447775,
0.326131 , 0.4879743 , 0.40387802, 0.36451519, 0.34205403,
0.4380145 , 0.42209148, 0.26836585, 0.40466779, 0.3113309 ,
0.39576034, 0.35685413, 0.39922502, 0.36962481, 0.31978173,
0.3962891 , 0.36759539, 0.3706756 , 0.41769948, 0.37093661,
0.47298534, 0.36451519, 0.34021348, 0.45451087, 0.33229141,
0.30798969, 0.39103519, 0.34179302, 0.30058964, 0.34866431,
0.5442388 , 0.41146694, 0.34021348, 0.31415009, 0.32823257,
0.38036608, 0.34637388, 0.34663489, 0.3274428 , 0.37473444,
0.34716365, 0.33871282, 0.49826569, 0.30904047, 0.32718179,
0.30798969, 0.30058964, 0.38370729, 0.45300347, 0.54202051,
0.32823257, 0.38573671, 0.408009 , 0.39110734, 0.45484402,
0.39549933, 0.38167787, 0.39437641, 0.31415009, 0.42385989,
0.35174451, 0.3144111 , 0.4689265 , 0.32921121, 0.39523832,
0.33255242, 0.37296602, 0.31644052, 0.3422429 , 0.33589363,
0.36451519, 0.35174451, 0.36680562, 0.32410158, 0.37525645,
0.40616845, 0.39136835, 0.32181115, 0.36248577, 0.28447775,
0.32076037, 0.42183047, 0.31106989, 0.31212067, 0.31952073,
0.36222476, 0.38986769, 0.33995247, 0.30596027, 0.36346441,
0.32718179, 0.30058964, 0.36019534, 0.35711514, 0.3484033 ,
0.4241209 , 0.30032863, 0.41567006, 0.36969696, 0.32384057,
0.36556597, 0.37525645, 0.36988582, 0.31670153, 0.40669721,
0.31741916, 0.36444305, 0.34401131, 0.33890169, 0.40590744,
0.31336032, 0.36654461, 0.32947222, 0.31336032, 0.34637388,
0.36248577, 0.30596027, 0.35711514, 0.35711514, 0.32410158,
0.36346441, 0.40079782, 0.38265651, 0.34761353, 0.37859767,
0.35200552, 0.29829921, 0.39294789, 0.30261906, 0.30058964,
0.3144111 , 0.38573671, 0.35050486, 0.40151545, 0.34100325,
0.31336032, 0.37735802, 0.27373649, 0.3144111 , 0.330523 ,
0.27576591, 0.26836585, 0.29521901, 0.41638769, 0.4781671 ,
0.40571857, 0.43238286, 0.31873095, 0.39726774, 0.34637388,
0.42288125, 0.3113309 , 0.42175832, 0.32286194, 0.35050486,
0.32286194, 0.30596027, 0.43257173, 0.30058964, 0.45052417,
0.35174451, 0.39313676, 0.38802714, 0.34126426, 0.40079782,
0.3678564 , 0.40721923, 0.34558411, 0.34558411, 0.36222476,
0.3366834 , 0.47095592, 0.38900577, 0.38960668, 0.3706756 ,
0.4166487 , 0.34663489, 0.30569926, 0.29724843, 0.35482471,
0.36962481, 0.48876408, 0.29829921, 0.33255242, 0.3422429 ,
0.28984838, 0.30904047, 0.34408345, 0.40590744, 0.30904047,
0.31336032, 0.34637388, 0.33589363, 0.31670153, 0.36248577,
0.34558411, 0.3274428 , 0.33897383, 0.3854757 , 0.47167354,
0.28650717, 0.28447775, 0.3484033 , 0.29521901, 0.30261906,
0.30366984, 0.35685413, 0.32384057, 0.32718179, 0.40676935,
0.38678749, 0.33995247, 0.28984838, 0.3144111 , 0.29521901,
0.30596027, 0.31873095, 0.31336032, 0.3113309 , 0.30798969,
0.31873095, 0.33484285, 0.33890169, 0.35174451, 0.39005656,
0.37191524, 0.31670153, 0.41893913, 0.3113309 , 0.40827001,
0.40086996, 0.34021348, 0.35940557, 0.37525645, 0.34126426,
0.38494693, 0.39136835, 0.41488029, 0.35606436, 0.31415009,
0.36943595, 0.31846994, 0.38141686, 0.36864618, 0.28447775,
0.31538974, 0.29521901, 0.36969696, 0.30904047, 0.330523 ,
0.39850739, 0.31336032, 0.30596027, 0.32181115, 0.3113309 ,
0.33484285, 0.36556597, 0.31670153])
5. Decision Tree Regressor
decision_tree_regressor = DecisionTreeRegressor(random_state=42)
decision_tree_regressor.fit(X, y)
DecisionTreeRegressor(random_state=42)
decision_tree_regressor.predict(X)
array([1. , 1. , 1. , 0.625 , 0.4075 ,
0.9 , 0.9 , 0.9 , 0.66666667, 0.85 ,
0.85 , 0.85 , 0.525 , 0.8 , 0.326 ,
0.8 , 0.475 , 0.7 , 0.46 , 0.7 ,
0.7 , 0.7 , 0.465 , 0.7 , 0.7 ,
0.7 , 0.66666667, 0.5 , 0.65 , 0.65 ,
0.45 , 0.65 , 0.6 , 0.396 , 0.6 ,
0.6 , 0.6 , 0.5 , 0.38333333, 0.5 ,
0.55 , 0.33 , 0.39 , 0.385 , 0.5 ,
0.5 , 0.5 , 0.5 , 0.28 , 0.35 ,
0.45 , 0.396 , 0.5 , 0.48 , 0.47 ,
0.5 , 0.365 , 0.45 , 0.45 , 0.45 ,
0.45 , 0.45 , 0.45 , 0.38333333, 0.42 ,
0.3175 , 0.29 , 0.42 , 0.4 , 0.4 ,
0.31 , 0.4 , 0.4 , 0.31 , 0.31 ,
0.66666667, 0.3175 , 0.4 , 0.35 , 0.30666667,
0.4 , 0.3 , 0.28 , 0.3 , 0.4075 ,
0.35 , 0.35 , 0.35 , 0.35 , 0.35 ,
0.295 , 0.35 , 0.275 , 0.256 , 0.325 ,
0.35 , 0.396 , 0.35 , 0.31666667, 0.275 ,
0.35 , 0.33 , 0.33 , 0.25 , 0.26 ,
0.25 , 0.30666667, 0.32 , 0.23 , 0.3 ,
0.3 , 0.3 , 0.3 , 0.25 , 0.26 ,
0.245 , 0.3 , 0.3 , 0.245 , 0.33 ,
0.3 , 0.256 , 0.31666667, 0.31666667, 0.35 ,
0.325 , 0.275 , 0.3 , 0.3 , 0.3 ,
0.3 , 0.25 , 0.28 , 0.24 , 0.396 ,
0.29 , 0.365 , 0.26 , 0.27 , 0.27 ,
0.245 , 0.27 , 0.26 , 0.29 , 0.22 ,
0.25 , 0.525 , 0.2075 , 0.25 , 0.25 ,
0.25 , 0.25 , 0.21666667, 0.25 , 0.33 ,
0.25 , 0.326 , 0.25 , 0.25 , 0.26 ,
0.25 , 0.256 , 0.25 , 0.396 , 0.25 ,
0.3175 , 0.25 , 0.25 , 0.225 , 0.275 ,
0.25 , 0.625 , 0.24 , 0.24 , 0.295 ,
0.24 , 0.24 , 0.24 , 0.23 , 0.465 ,
0.23 , 0.39 , 0.22 , 0.22 , 0.22 ,
0.46 , 0.22 , 0.25 , 0.31 , 0.31 ,
0.21 , 0.28 , 0.22 , 0.26 , 0.28 ,
0.245 , 0.33 , 0.31 , 0.23 , 0.3 ,
0.24 , 0.385 , 0.21 , 0.2 , 0.2 ,
0.2 , 0.4075 , 0.275 , 0.2075 , 0.24 ,
0.2 , 0.475 , 0.26 , 0.35 , 0.2 ,
0.2 , 0.275 , 0.21 , 0.29 , 0.2075 ,
0.256 , 0.21666667, 0.245 , 0.326 , 0.45 ,
0.21666667, 0.19 , 0.25 , 0.3175 , 0.2 ,
0.2 , 0.23 , 0.2 , 0.326 , 0.2 ,
0.2 , 0.5 , 0.2 , 0.30666667, 0.225 ,
0.2 , 0.3 , 0.2 , 0.19 , 0.38333333,
0.18 , 0.18 , 0.18 , 0.18 , 0.4075 ,
0.18 , 0.2075 , 0.25 , 0.28 , 0.22 ,
0.18 , 0.245 , 0.256 , 0.28 , 0.326 ,
0.19 , 0.25 , 0.23 ])
decision_tree_regressor.score(X, y)
0.7410570792901311
6. Validation
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=42)
decision_tree_regressor = DecisionTreeRegressor(random_state=42)
decision_tree_regressor.fit(X_train, y_train)
DecisionTreeRegressor(random_state=42)
decision_tree_regressor.score(X_train, y_train)
0.7325965837309238
decision_tree_regressor.score(X_test, y_test)
-1.0994712392955237
7. Conclusion
The Trap
The trap here is using same data for training and validation. As a beginner, it is common to look into a few models (here we looked into Linear Regression and Decision Tree Regressor), and concluded one is better than the other because the latter had a good determination coefficient score.
However, after validation we realize that the Decision Tree Regressor is up to no good.
The score is negative, and based on the documentation above:
The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse)
This is just a very basic example of misjudgement on my side. As a peer reviewer, you might feel like this is something very trivial. Finally, I just demonstrated one example here. There are pleanty of these in analytics.