Diffie-Hellman key exchange
(The introductory content is from wikipedia)
Diffie–Hellman key exchange is a method of securely exchanging cryptographic keys over a public channel and was one of the first public-key protocols as originally conceptualized by Ralph Merkle and named after Whitfield Diffie and Martin Hellman. DH is one of the earliest practical examples of public key exchange implemented within the field of cryptography.
Diffie-Hellman is a way of generating a shared secret between two people in such a way that the secret can’t be seen by observing the communication. That’s an important distinction: You’re not sharing information during the key exchange, you’re creating a key together.
This is particularly useful because you can use this technique to create an encryption key with someone, and then start encrypting your traffic with that key. And even if the traffic is recorded and later analyzed, there’s absolutely no way to figure out what the key was, even though the exchanges that created it may have been visible. This is where perfect forward secrecy comes from. Nobody analyzing the traffic at a later date can break in because the key was never saved, never transmitted, and never made visible anywhere.
The way it works is reasonably simple. A lot of the math is the same as you see in public key crypto in that a trapdoor function is used. And while the discrete logarithm problem is traditionally used (the xy mod p business), the general process can be modified to use elliptic curve cryptography as well.
But even though it uses the same underlying principles as public key cryptography, this is not asymmetric cryptography because nothing is ever encrypted or decrypted during the exchange. It is, however, an essential building-block, and was in fact the base upon which asymmetric crypto was later built.
Cryptographic explanation
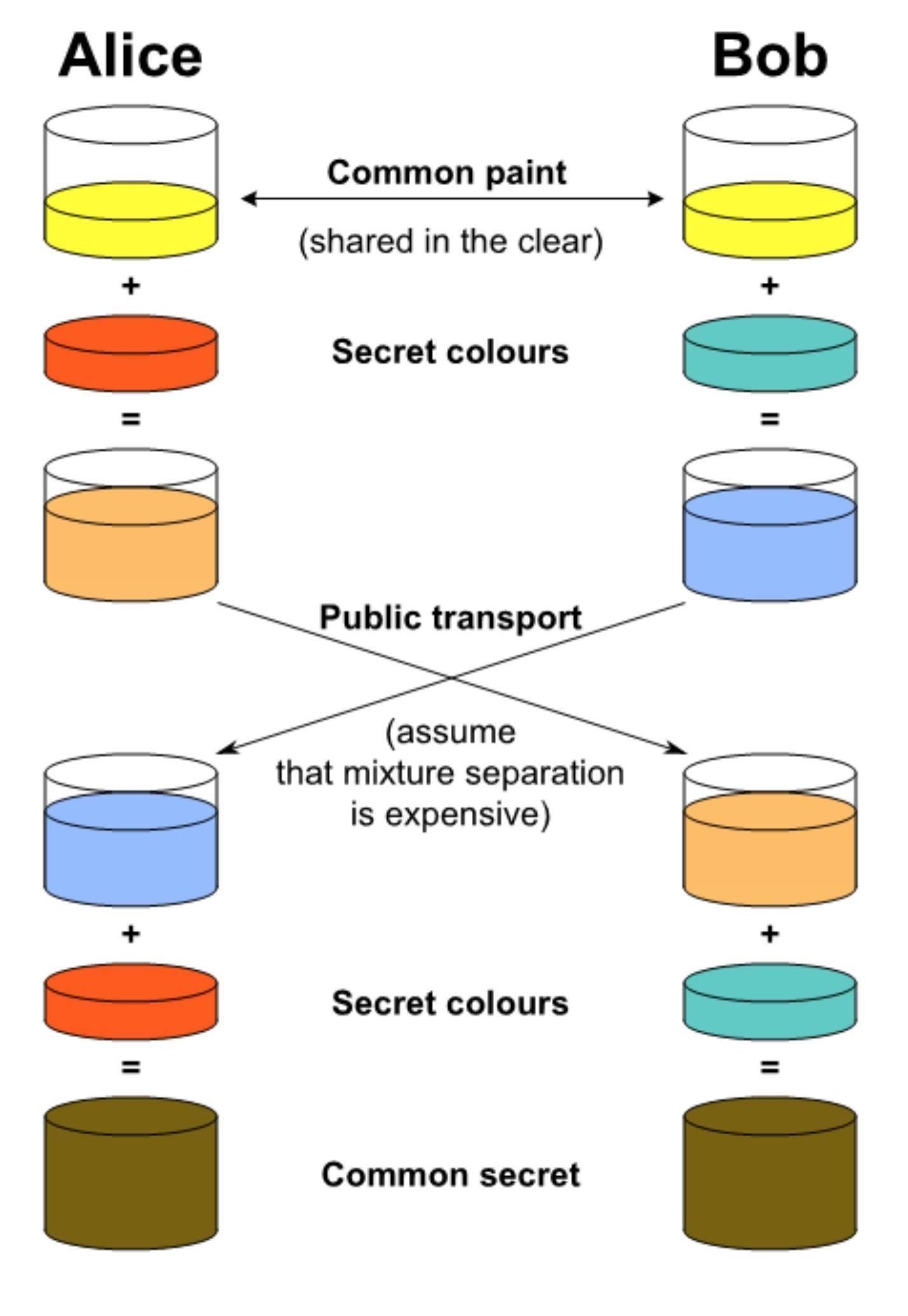
The simplest and the original implementation of the protocol uses the multiplicative group of integers modulo p, where p is prime, and g is a primitive root modulo p. These two values are chosen in this way to ensure that the resulting shared secret can take on any value from 1 to p–1. Here is an example of the protocol, with non-secret values in blue, and secret values in red.
Imports
import base64
from primesieve import nth_prime
from random import randint
from Crypto.Cipher import AES
Key Sharing
Public numbers
# small prime number
g = nth_prime(50)
g
229
# large prime number
p = nth_prime(1000)
p
7919
Alice and Bob
Private number
a = nth_prime(randint(1, p-1))
b = nth_prime(randint(1, p-1))
a
49019
b
70639
Public Message Transfer
Alice sends Bob publicly
alice_sends = g**a % p
Bob sends Alice publicly
bob_sends = g**b % p
Shared Secret key
Alice
shared_secret_key_alice = bob_sends**a % p
shared_secret_key_alice
7065
Bob
shared_secret_key_bob = alice_sends**b % p
shared_secret_key_bob
7065
assert shared_secret_key_alice==shared_secret_key_bob
shared_secret_key = shared_secret_key_alice
Both Alica and Bob now have the secret key, without compromising their private keys.
DH is public key/asymmetric crypto but not encryption. For the demo, AES 256 (takes 32 bytes)
Encryption and Decryption
Changing the key to 32 byte (a bad hacky way)
key = str(shared_secret_key)
key_bytes = str.encode(key.zfill(32))
# The message should be a multiple of the byte size
alice_to_bob_original = str.encode('hello world how are you'.zfill(256))
cipher = AES.new(key_bytes, AES.MODE_ECB)
cipher_msg = cipher.encrypt(alice_to_bob_original)
cipher_msg is sent to the server, bob reads the cipher_msg and uses the secret key to decipher
decipher = AES.new(key_bytes, AES.MODE_ECB)
print(decipher.decrypt(cipher_msg))
b'00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000hello world how are you'
DH is prone to man-in-the-middle attacks
The Diffie-Hellman Scheme does not provide authentication of any kind. It only allow 2 anonymous parties to share a common secret. But for all Alice knows, she could be shaking hands with the devil (instead of Bob). This is why we need at least one party to be authenticated.
For example: SSL (https), the webserver is authenticated using PKI (Public Key Infrastructure), and then a secure connection is established (D-H) between the website and the client. Since the website has been authenticated, the client can trust the website, but the website cannot trust the client. It is now safe for the client to provide his own authentication details on the webpage.
For a practical answer if you are configuring your SSL/TLS server: you should use a modulus of at least 2048-bit, and a generator g such that the order of g is a prime q of at least 256 bits; alternatively, you may use a modulus p which is a “safe prime” (the order of g will then be either a very big prime, or twice a very big prime, which is almost as good). Some people feel safer when they generate their DH parameters “themselves”(*) instead of reusing existing values; if that’s what it takes to allow you to sleep at night, then do it.
Elliptic Curve replaces primes with elliptic curve. The benefit is efficiency.