Snakes and Ladders

This game needs no introduction. Although there are several variations of this game (mainly on position of the snakes and ladders), the rules are generally the same. Some of the rules, (which are part of my algorithm) are mentioned below. Also, this game requires no skill as it solely depends on luck/probability. This allows several mathematical questions relating to this game be answered using Monte Carlo simulation. However, for this post, I will only be investigating from an analytic/subjective stand point. That is, I will be using Markov Chain to answer those questions. Markov Chain Wikipedia link
The game’s Markov property or memorylessness allows us to use Markov Chain. That is, the probability of occurrence of next event only depends on current event and not on any other events that occurred before. An example from our game: It does not matter if the player reached square 31 using the ladder from square 9, or by traversing the hard way around. Once the player is in 31, the probability of getting to square 32 does not depend on the “past”. Transition matrix Wikipedia link Transition matrix is a 2 dimensional array that encapsulates state transitional probabilities. For example, a transition matrix P, given the following information (Mathematical model of one dimensional random walk),

would be,

Transition matrix for Snakes and Ladders Trivial Transition Matrix
First of all, consider a case where there are no snakes or ladders. Let us call this our Trivial (for the lack of words) scenario.

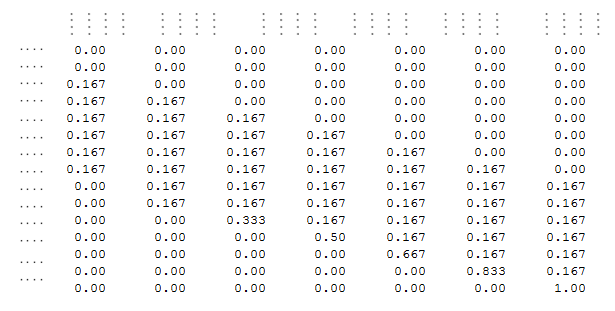
This definitely makes for a boring game. However, it helps with the math. First of all, the square 0 is the position the player is before the game starts. Now, since we are using a cubic die, on the first roll, the probability of going from 0 to 1, 0 to 2, 0 to 3, 0 to 4, 0 to 5, and 0 to six is 1/6. Since we are not accounting for snakes or ladders, the probability of going from box i to boxes i+1, i+2, i+3, i+4, i+5, and i+6 are all going to be 1/6, unless we run out of space. That is, if we are at 97, the person can only move to next step if the die rolls 1, 2 or 3. For anything greater, the person will not go to the next step. Therefore, in this case, the probabilities are: 97 to 98 = 1/6, 97 to 99 = 1/6, 97 to 100 = 1/6 and 97 to 97 = 3/6.
Building the Trivial transition matrix based on the aforementioned rule.
import Jama.Matrix;
/**
* @return 101X101 Transition Matrix for case: Trivial
*/
public Matrix trivialMatrix() {
int difference, playerPosition = 0, matrixSize=101;
double transitionM[][] = new double\[matrixSize\][matrixSize];
double probability = 1.0 / 6;
for (playerPosition = 0; playerPosition < transitionM.length; playerPosition++) {
for (int i = 1; i <= 6; i++) {
if ((difference = matrixSize - playerPosition) <= 6) {
for (int k = 1; k < difference; k++) {
transitionM\[playerPosition\][playerPosition + k] = probability;
}
transitionM\[playerPosition\][playerPosition] = (6 - difference + 1) * probability;
} else {
transitionM\[playerPosition\][playerPosition + i] = probability;
}
}
}
return new Matrix(transitionM);
}
Top-Left

Bottom-Right
Non-Trivial Transition Matrix

Snakes:
98 ~ 78, 95 ~ 75, 93 ~ 73, 87 ~ 24, 64 ~ 60, 62 ~ 19, 56 ~ 53, 49 ~ 11, 48 ~ 26, 16 ~ 6
Ladders:
1 ~ 38, 4 ~ 14, 9 ~ 31, 21 ~ 42, 28 ~ 84, 36 ~ 44, 51 ~ 67, 71 ~ 91, 80 ~ 100
I decided to use a simple List implementation for this. This might most likely be the Brute-Force implementation (I know several ways to make it better but none to make it worse). One way to make it more efficient would be to use 82 by 82 matrix instead of 101 by 101.
The advantage of using this implementation over the 82 by 82 matrix (apart from easy implementation) is that this method can be used for any snakes and ladders board variation. It also allows us to check for some hypothetical cases or answer more important questions. Eg: What is the best way to position snakes and ladders for maximum thrill to a player?
Building the non-Trivial transition matrix
/**
* @return 101X101 Transition Matrix for case: non-Trivial
*/
public Matrix nonTrivialMatrix() {
int playerPosition,matrixSize=101,difference;
List<Integer> from = Arrays.asList(1, 4, 9, 21, 28, 36, 51, 71, 80, 98, 95, 93, 87, 64, 62, 56, 49, 48, 16);
List<Integer> to = Arrays.asList(38, 14, 31, 42, 84, 44, 67, 91, 100, 78, 75, 73, 24, 60, 19, 53, 11, 26, 6);
double probability = 1.0 / 6;
double transitionM[][] = new double\[matrixSize\][matrixSize];
for (playerPosition = 0; playerPosition < transitionM.length; playerPosition++) {
if (!from.contains(playerPosition)) {
for (int i = 1; i <= 6; i++) {
if ((difference = 6 - playerPosition) <= 6) {
for (int k = 1; k < difference; k++) {
if (from.contains(playerPosition + k)) {
transitionM\[playerPosition\][to.get(from.indexOf(playerPosition + k))] = probability;
} else {
transitionM\[playerPosition\][playerPosition + k] = probability;
}
}
if (from.contains(playerPosition)) {
transitionM\[playerPosition\][to.get(from.indexOf(playerPosition))] = (6 - difference + 1) * probability;
} else {
transitionM\[playerPosition\][playerPosition] = (6 - difference + 1) * probability;
}
} else {
if (from.contains(playerPosition + i)) {
transitionM\[playerPosition\][to.get(from.indexOf(playerPosition + i))] = transitionM\[playerPosition\][to.get(from.indexOf(playerPosition + i))] + probability;
} else {
transitionM\[playerPosition\][playerPosition + i] = transitionM\[playerPosition\][playerPosition + i] + probability;
}
}
}
}
}
return new Matrix(transitionM);
}
Top-Left
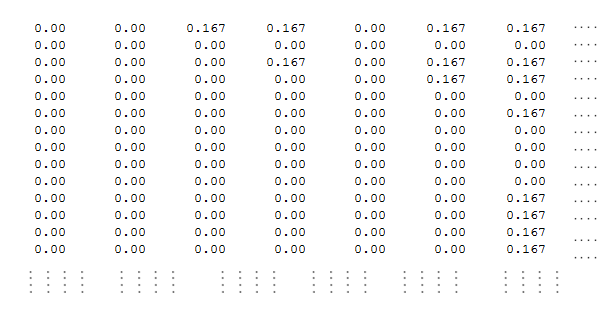
Bottom-Right
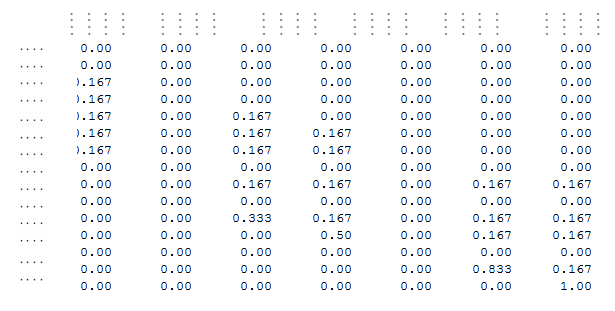
Probability Vector Wikipedia link
Probability vectors
represents the probability of being on a certain square after n dice rolls. It is a vector with non-negative entries that add up to one.
implies that the probability of being on square 0 is 1. This is our input.
……
If P is the Trivial transition matrix,
If P is the non-Trivial transition matrix.
Building the Probability Vector
/**
* @return Probability Vector with 1 being the first element
*/
public Matrix probabilityVector() {
double probabilityV[] = new double[101];
probabilityV[0] = 1;
return new Matrix(probabilityV, 1);
}
Question 1: Probability of being on square s after n dice rolls: Using Vn-1 * P = Vn
/**
* @param transitionMatrix
* @param probabilityVector
* @param diceRolls
*/
public static void squareProbability(Matrix transitionMatrix, Matrix probabilityVector, int diceRolls) {
NumberFormat nf = NumberFormat.getInstance();
nf.setMinimumFractionDigits(20);
System.out.println("Dice rolls: "+diceRolls);
for (int i = 1; i <= diceRolls; i++) {
probabilityVector = probabilityVector.times(transitionMatrix);
}
probabilityVector.print(nf, 3);
}
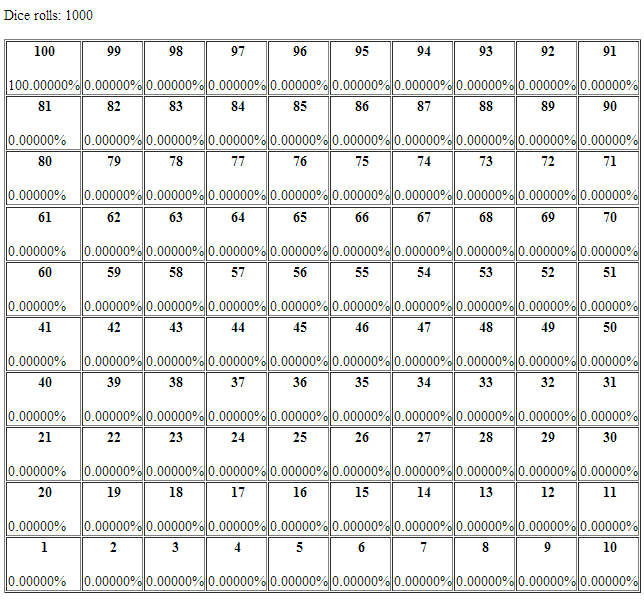
Some outputs for the Trivial matrix: I used html tables to simulate the board (basically printed the html tags within java code).
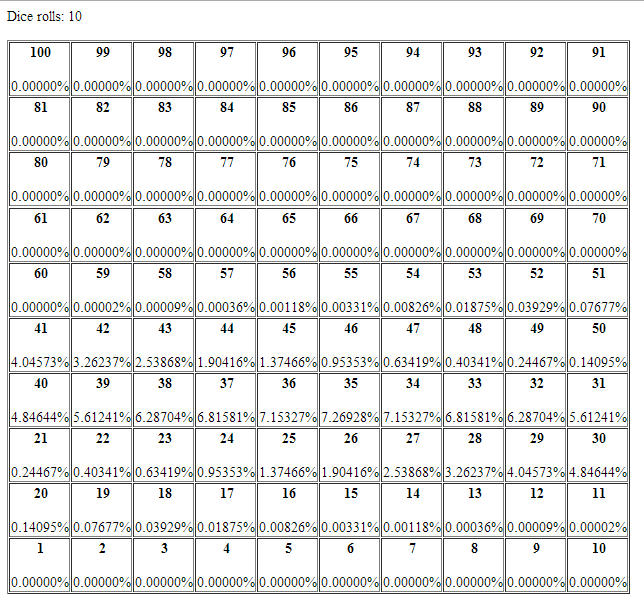
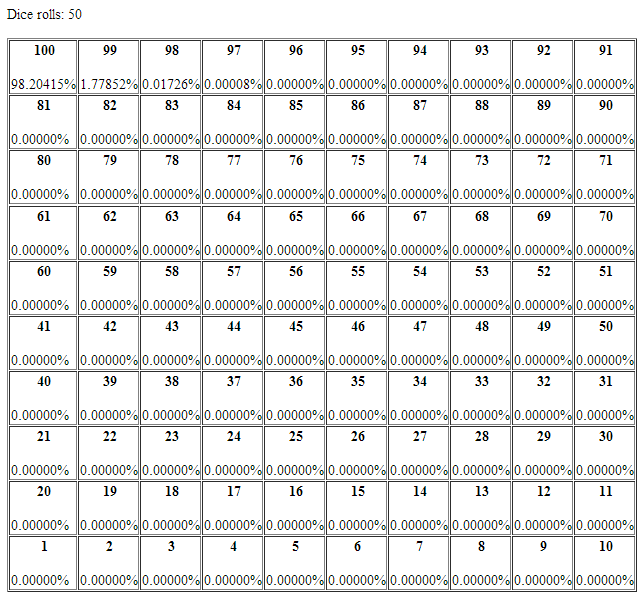
Some outputs for the non-Trivial matrix:




Question 2: Minimum length of a game and occurrence probability That is, after how many n, is the probability at square 100 greater than 0 for the first time?
For the trivial case, the answer is, ceiling of 100/6 = 17.
For the non-trivial case,
/**
* @param transitionMatrix
* @param probabilityVector
*/
public static void gameCompletion(Matrix transitionMatrix, Matrix probabilityVector) {
NumberFormat nf = NumberFormat.getInstance();
nf.setMinimumFractionDigits(30);
int box = 100;
int diceRolls = 0;
while (probabilityVector.get(0, box) == 0) {
diceRolls++;
probabilityVector = probabilityVector.times(transitionMatrix);
}
System.out.println("The game can be completed in min of " + diceRolls + " dice rolls.");
System.out.println("Probability of it happening: " + nf.format(probabilityVector.get(0, box)));
}
Results:
Non-Trivial Matrix
The game can be completed in min of 7 dice rolls.
Probability of it happening: 0.001564643347050754000000000000
Rolls of {4,6,6,2,6,4,6} is one shortest solution. However, in theory, the game could last forever. Therefore, there is no longest game.
Trivial Matrix
The game can be completed in min of 17 dice rolls.
Probability of it happening: 0.000000000009038995585604526000
Rolls of {6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6} is the only shortest solution. Longest game in this case is 100 dice rolls. The player will have to roll 1, 100 consecutive times from start. Question 3: Expected length of a game: Let subStochasticMatrix be the 100 by 100 matrix obtained by deleting the last row and column of the transition matrix. Also, let I be 100 by 100 identity matrix. Let inverse be the inverse of the difference of I and subStochasticMatrix. The expected number of rolls is given by the sum of entries in top row of the matrix inverse.
/**
* @param transitionMatrix
* @param probabilityVector
*/
public static void expectedLength(Matrix transitionMatrix, Matrix probabilityVector){
Matrix subStochasticMatrix=transitionMatrix.getMatrix(0, 99, 0 ,99);
Matrix I = Matrix.identity(100,100);
Matrix inverse = (I.minus(subStochasticMatrix)).inverse();
double sum=0;
for (int i =0;i<=99;i++){
sum=sum+inverse.get(0, i);
}
System.out.println("Expected game length: "+sum);
}
Results:
Non-Trivial Matrix
Expected game length: 39.59836564020812
Trivial Matrix
Expected game length: 33.33333333333334