[Paper Exploration] Statistical Modeling: The Two Cultures
Abstract
There are two cultures in the use of statistical modeling to reach conclusions from data. One assumes that the data are generated by a given stochastic data model. The other uses algorithmic models and treats the data mechanism as unknown. The statistical community has been committed to the almost exclusive use of data models. This commitment has led to irrelevant theory, questionable conclusions, and has kept statisticians from working on a large range of interesting current problems. Algorithmic modeling, both in theory and practice, has developed rapidly in fields outside statistics. It can be used both on large complex data sets and as a more accurate and informative alternative to data modeling on smaller data sets. If our goal as a field is to use data to solve problems, then we need to move away from exclusive dependence on data models and adopt a more diverse set of tools.
Author: Leo Breiman
Published on 2001
Leo Breiman

- Leo Breiman was an influential American statistician and professor, best known for his significant contributions to the field of statistics and machine learning.
- Breiman made significant contributions to various areas of statistics, including classification and regression trees, ensemble learning methods, and random forests.
- One of Breiman’s most notable contributions is the development of the Random Forest algorithm, introduced in his seminal paper “Random Forests” published in 2001.
- His ideas continue to be studied, extended, and applied in various domains, contributing to the advancement of data science and predictive modeling.
The Two Cultures
- Statistics start with data
- Nature functions to associate the predictor variables with the response variables
- There are two goals in analyzing the data:
- Prediction: To be able to predict what the responses are going to be to future input variables
- Information: To extract some information about how nature is associating the response variables to the input variables.
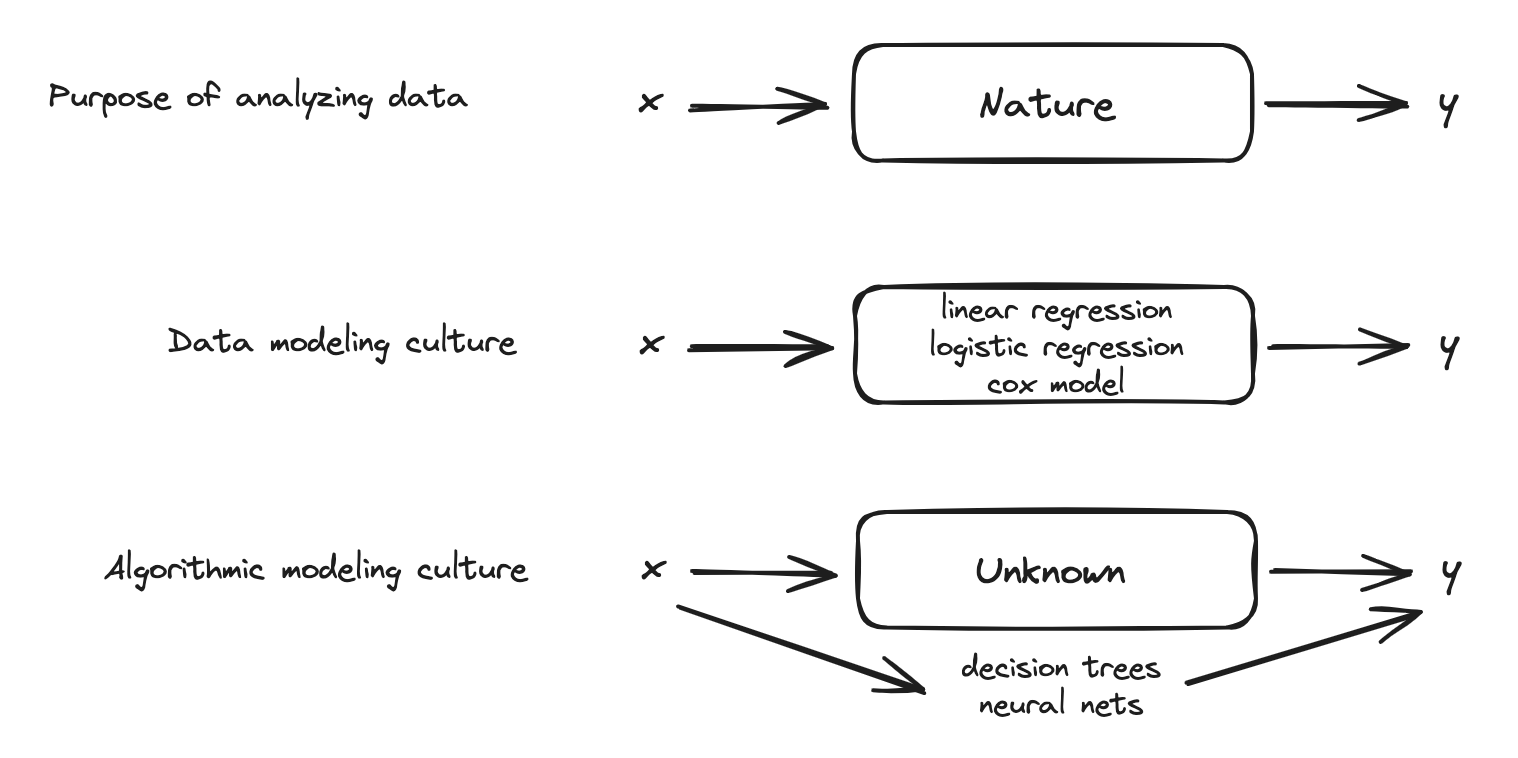
The Data Modeling Culture
- The analysis in this culture starts with assuming a stochastic data model for the inside of the black box
- Response variables = f(predictor variables, random noise, parameters)
- The values of the parameters are estimated from the data and the model then used for information and/or prediction.
- Model validation. Yes–no using goodness-of-fit tests and residual examination.
- Estimated culture population. 98% of all statisticians.
The Algorithmic Modeling Culture
- The analysis in this culture considers the inside of the box complex and unknown.
- Their approach is to find a function fx—an algorithm that operates on x to predict the responses y.
- Model validation. Measured by predictive accuracy.
- Estimated culture population. 2% of statisticians, many in other fields.
Motivation (Why review this paper?)

- I graduated with a Bachelors in Mathematics when the algorithmic modeling culture was not commonplace.
- I graduated with a Masters in Machine Learning at a time where the algorithmic modeling culture everywhere.
- I work in a company that delivers Deep Learning solutions, but requires data modeling culture for its own solution-ing (experimentation, distribution, sampling, etc.).
- I work with students in Nepal who want to implement Large Language Models, sophisticated Deep Learning Models, but do not want to learn about foundational statistics/linear algebra/calculus/optimization.
- In many ways, I am currently trying to ask students in Nepal to do the exact opposite of what Breiman had to do with this paper. The 98%-2% might have flipped on its head. I do not like it.
For the last point, I am not implying that prediction accuracy is not important, or should not be pursued. I am implying that it is not the only thing to be pursued. That persuasion has several shortcuts with the advancement of ML packages. This not only makes the data model a black box, but also make the machine learning implementation a black box.
Breiman’s call to statisticians to join the 2%
- Breiman argues that the focus in the statistical community on data models has:
- Led to irrelevant theory and questionable scientific conclusions
- Kept statisticians from using more suitable algorithmic models
- Prevented statisticians from working on exciting new problems
Breiman as a consultant
- Breiman’s experiences as a consultant formed his views about algorithmic modeling
- Breiman’s perceptions on Statistical Analysis:
- Focus on finding a good solution—that’s what consultants get paid for.
- Live with the data before you plunge into modeling.
- Search for a model that gives a good solution, either algorithmic or data.
- Predictive accuracy on test sets is the criterion for how good the model is.
- Computers are an indispensable partner
Breiman after returning to University
I had one tip about what research in the university was like. A friend of mine, a prominent statistician from the Berkeley Statistics Department, visited me in Los Angeles in the late 1970s. After I described the decision tree method to him, his first question was, “What’s the model for the data?”
Upon my return, I started reading the Annals of Statistics, the flagship journal of theoretical statistics, and was bemused. Every article started with: Assume that the data are generated by the following model: …
Rashomon Effect and the Data Modeling Culture
Occam’s razor and the Data Modeling Culture
Occam’s razor is a principle often attributed to 14th–century friar William of Ockham that says that if you have two competing ideas to explain the same phenomenon, you should prefer the simpler one.


Side note. Check this amazing article on mental models
The curse of dimensionality the Data Modeling Culture
As the number of features or dimensions grows, the amount of data we need to generalize accurately grows exponentially!
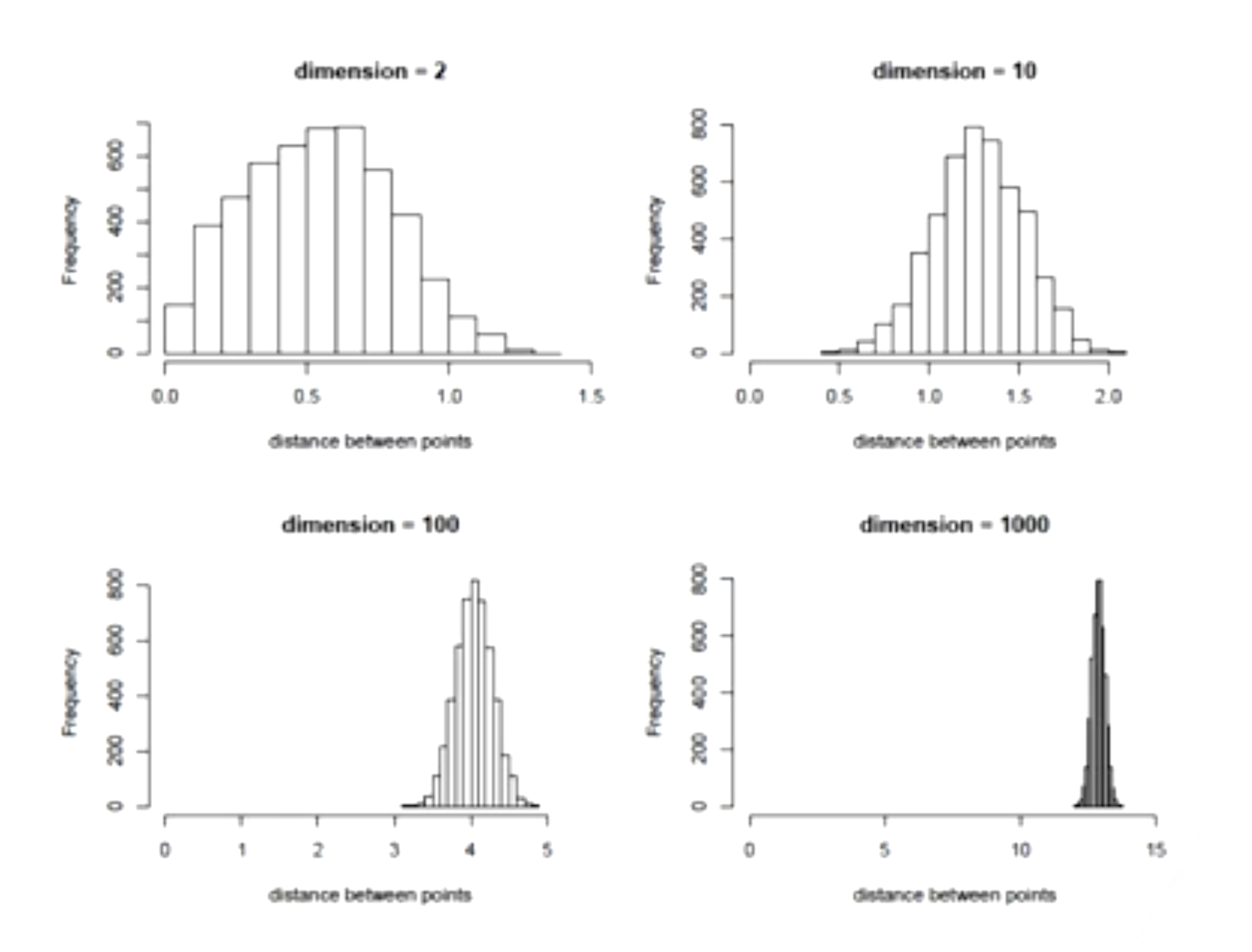
As distance between observations increases with the dimensions, the sample size required for learning a model drastically increases.
- Increased Sparsity: In higher dimensions, the available data points are spread out more thinly across the space. This means that data points become farther apart from each other, making it challenging to find meaningful clusters or patterns. It’s like having a lot of points scattered in a large, high-dimensional space, and they’re so spread out that it’s difficult to identify any consistent relationships.
- More Data Needed: With higher-dimensional data, you need a disproportionately larger amount of data to capture the underlying patterns accurately. When the data is sparse, it’s harder to generalize from the observed points to make accurate predictions or draw conclusions. As the dimensionality increases, you might need exponentially more data to maintain the same level of accuracy in your models.
- Impact on Complexity: The complexity of machine learning models increases with dimensionality. More dimensions mean more parameters to estimate, which can lead to overfitting – a situation where a model fits the training data too closely and fails to generalize well to new data.
- Increased Computational Demands: Processing and analyzing high-dimensional data require more computational resources and time. Many algorithms become slower and more memory-intensive as the number of dimensions grows. This can make experimentation and model training more challenging and time-consuming.
- Difficulties in Visualization: Our ability to visualize data effectively diminishes as the number of dimensions increases. We are accustomed to thinking in 2D and 3D space, but visualizing data in, say, 10 dimensions is practically impossible. This can make it hard to understand the structure of the data and the relationships between variables.
Conclusion
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
...
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
random_forest = RandomForestClassifier(n_estimators=100, random_state=42)
random_forest.fit(X_train, y_train)
y_pred = random_forest.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)